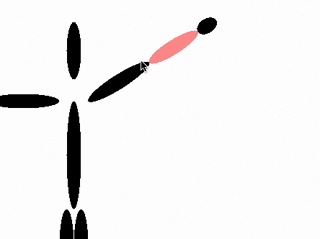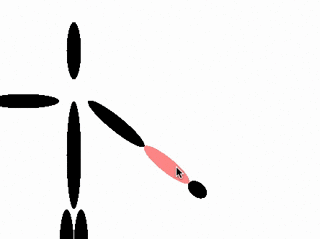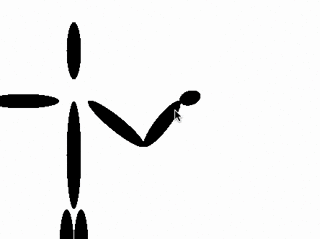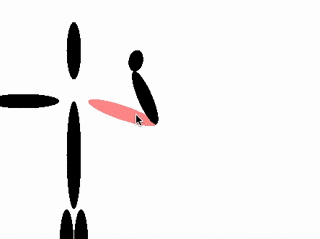Simple Inverse Kinematics
In computer animation, people often work with "puppets" that you can pose and manipulate. There are a few different ways that this happens. The easiest one to program is called forward kinematics, and it looks like this:
Demo of forward kinematics
When you drag the upper arm of the puppet armature, the lower arm and hand follows. When you drag the lower arm, the hand follows. Nothing follows the hand. The changes propagate forward. This is pretty simple to program: when drawing the descendents of one segment of the armature, you just keep adding to the previous coordinate space. If the upper arm is rotated 20 degrees, when you are going to draw the lower arm, you don't rotate it back - you just keep that rotation and add to it.
There's another way of posing puppet armatures, and it's called inverse kinematics. It looks like this:
Demo of inverse kinematics
In inverse kinematics, you drag the hand, and it bends the other joints accordingly to make everything line up. The transforms are propagated backwards from before, from the hand to the upper arm. This tends to be more natural for artists to work with so it's a worthwhile enhancement to add to an animation system. Programming it is a little harder though.
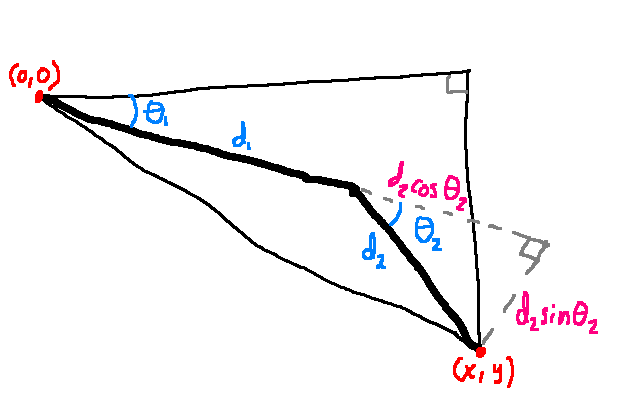
You might want to attempt to compute the angles algebraically. Given a mouse coordinate (x,y), an upper arm with length d1 and angle θ1, and a lower arm with length d2 and angle θ2, you have yourself a trig problem that you can solve:
This gets messy fast, and I forgot all my trig identities after first year :'(
This is doable for a length-2 chain of joints, but becomes really tedious for anything more than that (or if you add a third dimension, since 3D models need IK as well). Instead, we can come up with a numerical solution that, over a few iterations, approximates the result for arbitrarily many joints. I'm going to describe an algorithm called Cyclic Coordinate Descent.
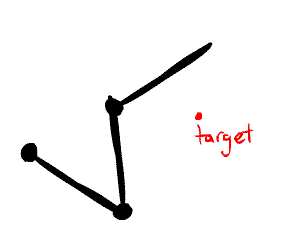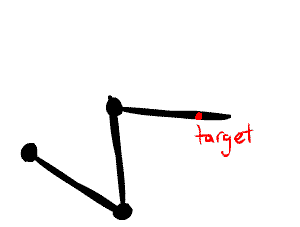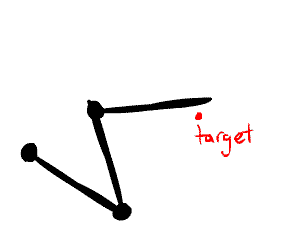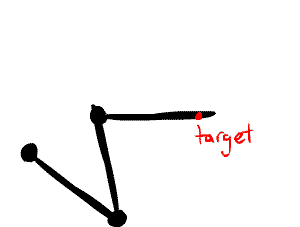
Here's the gist of the algorithm:
- Start at the lowest level joint (e.g. the hand, in the above examples)
- Angle that joint so that the line drawn from the base of the joint to the end of the chain points towards the target
- Go up to the next joint and do it again until there are no more joints
Visually, here's what that looks like:
One iteration of the IK algorithm pointing a joint chain at a target
In code, the most difficult part of this is figuring out where to point a given joint. We know we want to get the angle between the start of the joint to the end of the chain, but we need to do a little work to get that when the child joints are defined relative to their parent. The key is to take the endpoint from the lowest-level joint, and then apply the transform of that joint when passing it up to the parent. As we pass the endpoint up, joint to joint, we keep adding on to its transformation. This works much the same way forward kinematics works, except we start from the lowest level and work up.
When programming it, we usually don't have direct access to the lowest-level joint. Instead, higher-level joints have references to their children. With a setup like that, we just need to run the algorithm in post-order: before updating the current joint, tell the child to update. This way, we end up waiting for the most deeply nested joint to finish before working our way back up.
If we have a Bone object with x, y, angle, length, and child properties, the algorithm might look like this:
// takes in: a target point in the parent coordinate space
// returns: the endpoint of the chain, in that same parent
// coordinate space
function updateIK(target) {
// convert from parent to local coordinates
const localTarget = rotatePoint(translatePoint(target, -this.x, -this.y), -this.angle);
let endPoint;
if (this.child) {
endPoint = this.child.updateIK(localTarget);
} else {
// base case: the end point is the end of the current bone
endPoint = [this.length, 0];
}
// point towards the endpoint
const shiftAngle = angle(localTarget) - angle(endPoint);
this.angle += shiftAngle;
// convert back to parent coordinate space
return translatePoint(rotatePoint(endPoint, this.angle), this.x, this.y);
}
You will want to run the updateIK function a few times. Each iteration should bring it closer to the desired result, eventually converging as the number of iterations goes to infinity.
I've gone and made a demo in P5.js so you can see how the code works and play around with it. Feel free to check out the source code on CodePen.