Volumes and Subsurface Scattering
To render anything for use in film, you'll want to have more advanced materials than just the ones I described in my last post about 3D rendering. Those materials only take into account light colliding with objects at their surfaces. In reality, many objects interact with light more complexly than that. Have you ever held your hand up to a light source and seen your fingers glow red? Clearly, the light from behind your hand makes its way through your fingers to your eyes somehow, and our previous system doesn't let us do that. We'll need to add it in order to be able to render humans convincingly. So, let's talk about how that works.
Volumes
Let's start by modelling clouds. They're the prototypical example of something that only partially lets light through. In real life, clouds are made of a bunch of tiny particles. Any light that goes in may or may not hit one of the particles in the cloud, and the chance that it does hit something is proportional to how dense the particles are in the cloud. Materials like this that are filled with some density of particles are typically referred to as volumes in rendering. There's an element of randomness involved, so to get a good final image, you cast photons multiple times and average the results to get a convincing final image. Although it's not fast, it is still useful as a ground truth to compare with when testing approximations, so that's how we're going to build our volumes.
So, we have a photon heading through a volume on its way to the camera. The question we have to answer is how far in it goes before it hits a particle and bounces, if at all.
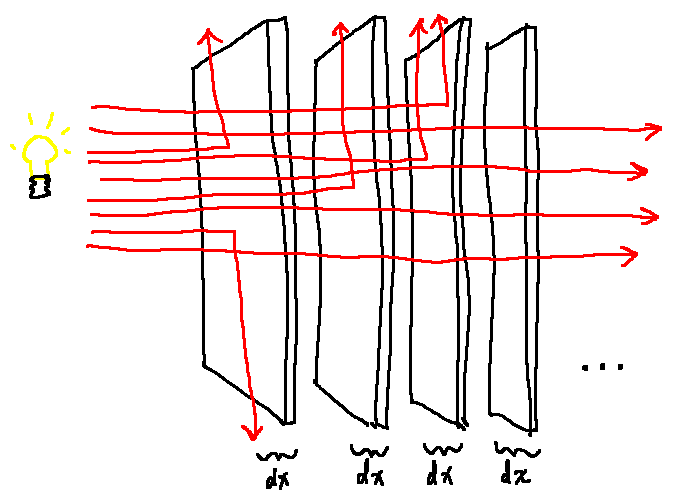
One way to solve this is to model the distances photons go as an exponential distribution. I didn't pull this distribution out of nowhere: we can divide the volume into a bunch of strips of particles that the light must pass through, one after the other. Each strip lets some percentage of photons through based on how dense the slice is with particles. Out of the photons that make it through, another percentage of that is let through the next slice. In the next slice, again, a percentage is let through. The result is an exponential decay of particles passing through, forming an exponential distribution of distances photons travel. This is called the Beer-Lambert Law.
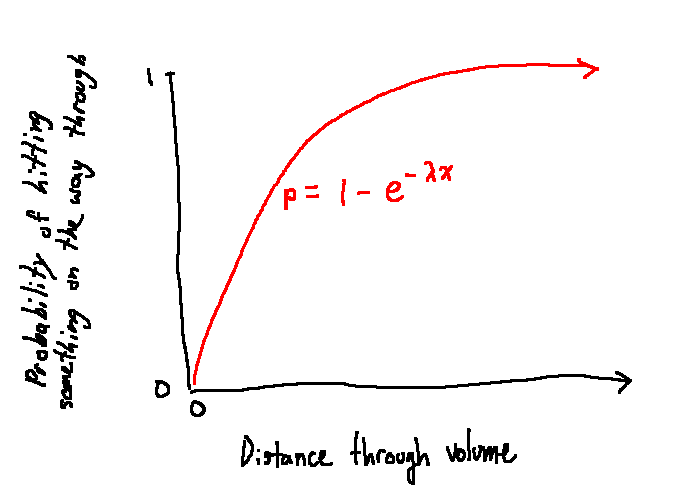
We'll define a property \(\lambda\) of the volume, where \(\lambda\) is a collision rate per unit distance. This is used in the cumulative distribution function (or "CDF") of an exponential distribution, \(p = 1 - e^{-\lambda x}\). The CDF tells us the probability that a photon heading into the volume for a distance \(x\) will hit a particle on the way. If we look at the graph, we see it starts at \((0,0)\). This makes sense: it tells us that if the photon goes a distance of 0 through the volume, there is no chance of it hitting anything. The graph goes to an asymptote of 1 as the distance goes to infinity, which tells us that if a photon goes through a volume longer and longer, it becomes ever closer to certain that it will hit something at some point.
With this equation, if we're given a distance the photon travels, we can figure out the probability of it making it that far. But that's the opposite of what we want when we are throwing the photons instead of observing them: we want to generate a random value and see how far the photon goes. We want the inverse of this graph: given a random value between 0 and 1, we want to find a distance from 0 to infinity representing the distance the light travels. If we rearrange the CDF for the distance \(x\), we find that we get \(\frac{-\ln(1 - p)}{\lambda}\). Since \(1 - p\) is a value between 0 and 1, we can replace it with a uniform random variable between 0 and 1. Code that looks like -ln(rand())/lambda will generate the distance travelled through the volume.
If the distance generated is greater than the distance the photon needs to go through to escape the volume, then we say it went all the way through without any collisions. Otherwise, it went our generated distance, and then hit a particle. After moving the photon, we dim its colour the same way as we would have if it hit a regular solid object. After averaging multiple samples, including both the times when the photon hits nothing and the times when it bounces, we end up with a blurry looking fog. So here's out algorithm:
- Calculate the distance the photon has to go through the volume, following its current path
- Generate a random distance the photon travels according to our exponential distribution
- If the distance is less than the length it must go through to exit the volume:
- Move that distance
- Adjust the direction of the photon (scatter it)
- Adjust the color of the photon (make it lose energy)
- Go back to step 1
- Otherwise, move the photon out of the volume and let it continue on its path
With that, you get volumes that look something like this:
Subsurface Scattering
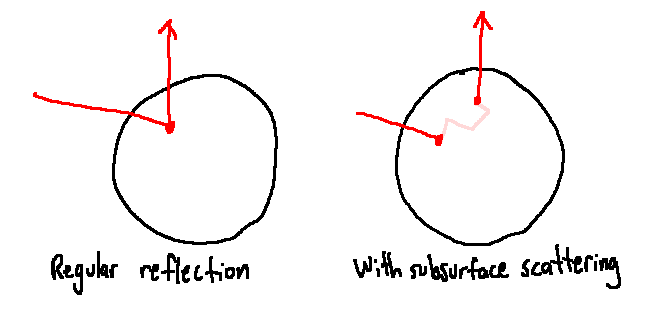
All of this relates to that phenomenon of glowing fingers because of something called subsurface scattering. As the name implies, some photons go through the surface of our fingers, get scattered when inside, and pop out somewhere else. From the outside of the object, it looks like the light hits the object, but instead of bouncing off from the point of collision, it bounces off from a point with a random offset from the point of collision. This is because the inside of the object has particles that photons bounce off of before exiting. The effect of this is that every photon that goes into the object also influences points some distance away. The light from the sun behind your finger can still influence the colour of the front of your finger because of this, despite it not being directly illuminated.
I implemented objects with subsurface scattering as a skin and a dense volume within it. The skin randomly lets some photons through into the volume within. The volume then scatters the photon, and after bouncing a few times, by the time the photon exits the volume, it has been randomly offset from its entry point. After the photon exits the volume, I bounce it as if the photon had just hit the surface at this new location.
Here's a gif of a sphere with subsurface scattering for its material being toggled on and off, for comparison:
As usual, the code for this is available on Github if you want to check out my implementation.