Differentiable Shadow Rendering

We extended the differentiable renderer Soft Rasterizer to support the rendering of soft shadows.

Background: differentiable rendering

There is a whole subfield of computer graphics and computer vision called inverse graphics, where instead of trying to realistically render a scene of your creation, you try to reconstruct a representation of a scene given an image of the scene. This is typically done by starting with an initial guess of the shapes in the scene, the materials, the lights, and the camera, and rendering an image. You then compare the rendered image with the target image, and call the magnitude of the difference the "loss." If the rendering is done in such a way that you can take the derivative of each pixel with respect to any of the scene parameters, then you can compute the gradient of the loss with respect to all those scene parameters. You can adjust each parameter by stepping them in the direction of the gradient, moving them slightly in the direction that would reduce the loss.

The difficult part is creating a rendering system that has derivatives. To figure out the colour of a pixel, a typical rendering system will send a ray from the camera through each pixel's location in the image plane to see what it hits in the scene. Imagine there are two boxes, one in front of the other, each a different colour. The pixel will be the colour of the box in the front. If you move the front box over, the pixel will continue to be the front box's colour until the moment it moves far enough that the rear box becomes visible, at which point the pixel suddenly takes on the colour of the rear box. Because the shift is immediate and discontinuous, the derivative isn't defined here. To compensate, differentiable renderers will typically make objects slightly blurry so that the transition is smooth and has a derivative everywhere. As optimization progresses, one can slowly reduce the blurriness to refine the level of detail being optimized in the image.

Our work is motivated by the cover of the book Gödel, Escher, Bach, which features blocks whose shadows appear to be different letters when seen from different sides. Could one create target shadows, and then optimize the shape of the blocks such that they create those shadows?

The cover of Gödel, Escher, Bach. Given the shadow shapes, we would like to compute the shape of the blocks.

It seems that most differentiable rendering systems either use very approximate rendering that does not take into account realistic shadows, or the rendering system performs detailed, physically-accurate lighting, which is much more computationally expensive. We aim to find a middle ground by adding support for fast, approximate soft shadows to a differentiable renderer.

Traditional shadow mapping

Hard shadows occur when a light source is a single point. A fragment is fully lit when there is an uninterrupted path between the fragment and the light. If there is an interruption, then it is in shadow.

A fast way to render shadows is to first render an image from the perspective of the light. For each pixel, instead of recording a colour, we record the distance to the closest object. This is called a depth map. Then, when rendering the real image, to see if a given fragment is in shadow, one simply needs to check if the distance from the fragment to the light is greater than the recorded distance for its angle to the light in the depth map.

To make this process differentiable, two changes need to occur:

1. The calculation of the closest distance to the light needs to be made smooth
2. The check of whether a given fragment is farther than the recorded closest distance needs to be made smooth

To solve the first problem, rather than taking the hard minimum distance, we use a soft minimum distance, which looks like this:

\(d_{min} = \frac{1}{\sum_i \exp(1/(\gamma d_i))} \sum_i d_i \exp(1/(\gamma d_i))\)

Here, the \(\gamma\) term represents the sharpness of the soft minimum. If one increases it to infinity, the formula converges on a true hard maximum.

To solve the second problem, we blur the depth map before looking up the closest depth. This means that in our gradient, nearby closest depths have an influence. This makes sense, because if one were to move the light slightly, then we would expect the closest depths to change accordingly. Finally, instead of doing a hard yes-or-no check to see if a depth value is greater than the one stored in the depth map, we use a sigmoid activation, again with tunable sharpness.

Hard shadows, rendered differentiably

Soft shadows

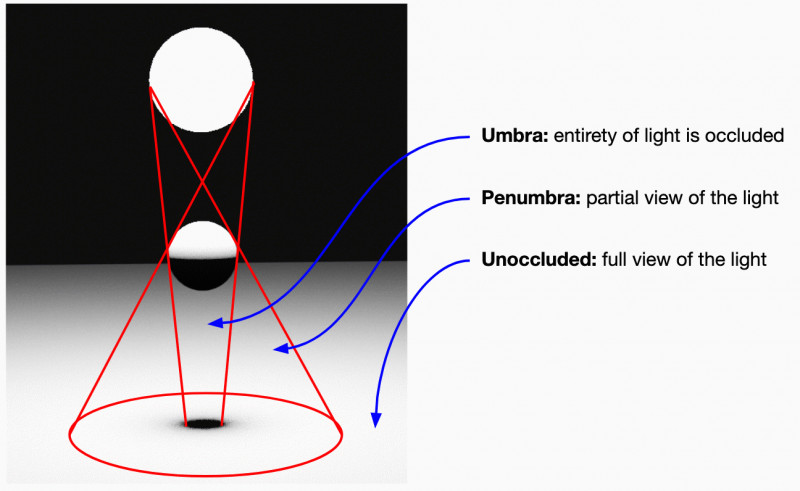
Soft shadows occur when a light source isn't just a point and instead has some surface area. If a fragment has an uninterrupted view of the entire light source, then it is fully lit. If the entire light source is hidden from the perspective of the fragment, it is in full shadow. If it has a partial view, then it is partially shaded. The area that sees a partial view of the light is called the penumbra of the light.

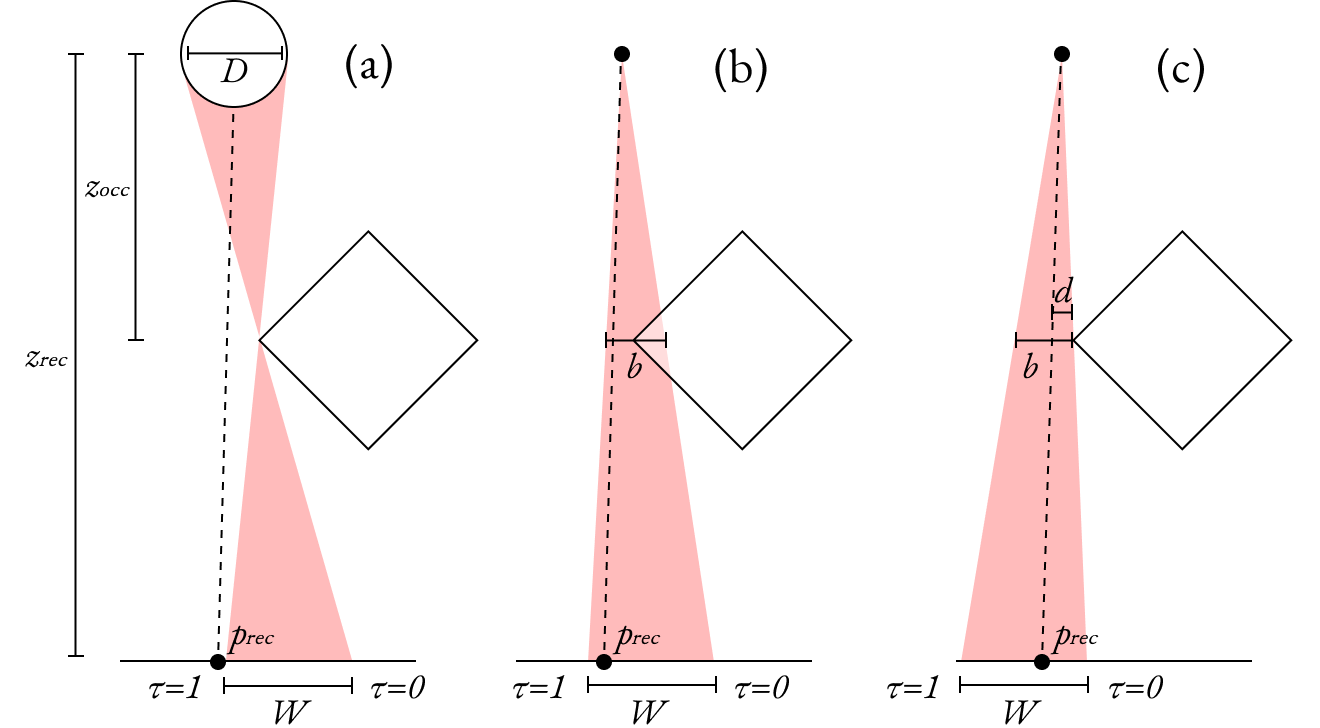
We are interested in a fast approximation of this penumbra which can be used in conjunction with a shadow map. To do this, we approximate sphere lights with single points. The true width of the penumbra region due to an occluder can be calculated, and then that can be used to construct a cone between the receiving fragment and the light source. At the inner edge of the cone, there is full shadow. At the other end, there is full brightness.

Point light sources are approximated as a sphere light with diameter D, whose true penumbra has a width W (a). The same penumbra size is used to create a cone representing the penumbra, with both inner and outer penumbras (b), and with just an outer penumbra (c).

If the penumbra extends out from the shadow that would exist from a point light, in order to tell where a fragment exists within the cone, one needs to take the line between the fragment and the center of a light and see how far away the occluder is from this line. If that distance is \(d\) and the width of the cone at that depth is \(b\), then the occlusion is \(d/b\).

When there are multiple partial occluders in front of a fragment, one would take the minimum of these occlusion values. Since this is not differentiable, we instead do a \(\text{softmin}(d/b)\) over all \(d\) and \(b\).

To render an image, we need to combine these partial occlusion values with the shadow map. Given:

• \(w\): a distance Gaussian weight based on how far away on the shadow map we look;
• \(s\): sigmoid of the difference between the distance from the fragment to the light and the distance from the light to the closest object; and
• \(\tau\): the penumbra term at the current fragment,

then the final shadow multiplier is:

\(\frac{\sum w\tau s}{\sum w}\)

This is a weighted sum of \(\tau s\), which can be interpreted as the amount of light if the fragment is in front, multiplied by the probability that it is in fact in front.

Hard shadows extended with a soft penumbra, rendered differentiably

Future work: evaluation

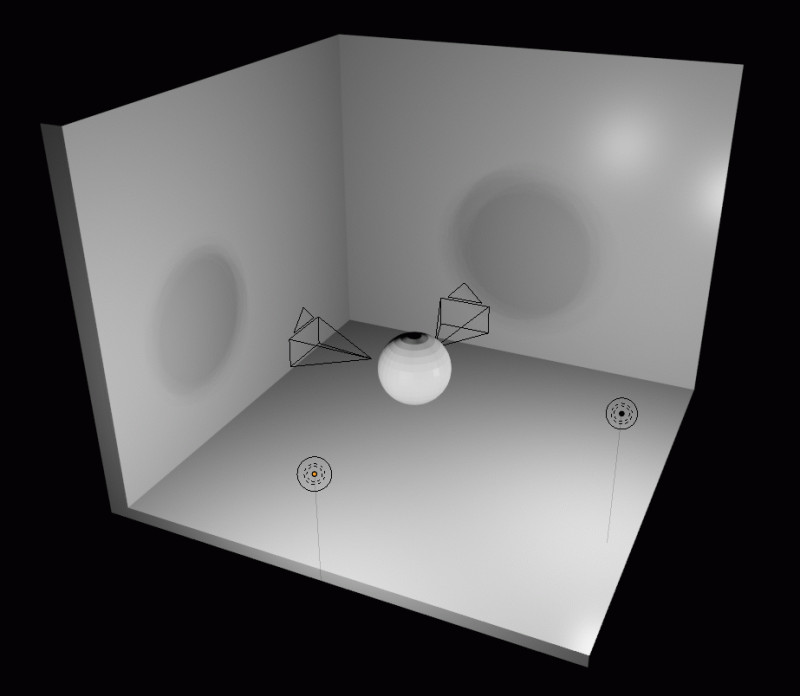
To evaluate how well this works, we set up a test scene where we ask to optimize a mesh, starting as a sphere, based on what two cameras can see. However, the cameras are not pointed at the mesh itself. Instead, it is pointed at the walls, where it can see shadows from two light sources.

Optimization of the sphere based only on what the cameras can see: its shadow from two angles

Unfortunately, we have not yet finished programming the derivatives into our custom CUDA kernel, so this will have to be run for real at a later date :')